Melles Griot Optics Guide - The Reflection of Light

Coating Theory

The Reflection of Light

Reflections at Uncoated Surfaces
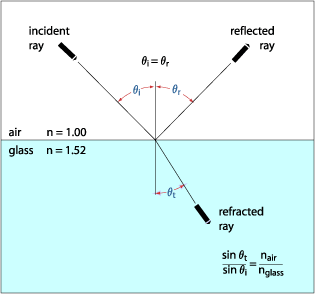
Whenever light is incident on the boundary between two media, some light is reflected and some is transmitted (undergoing refraction) into the second medium. Several physical laws govern the direction, phase, and relative amplitude of the reflected light. For our purposes, it is necessary to consider only polished optical surfaces. Diffuse reflections from rough surfaces are not considered here. The law of reflection states that the angle of incidence equals the angle of reflection. This is illustrated in the figure below, which shows reflection of a light ray at a simple air/glass interface. The incident and reflected rays make an equal angle with the axis perpendicular to the interface between the two media.

Reflection and refraction at a simple air/glass interface
Intensity
At a simple interface between two dielectric materials, the amplitude of reflected light is a function of the ratio of the refractive index of the two materials, polarization of the incident light, and the angle of incidence. When a beam of light is incident on a plane surface at normal incidence, the relative amplitude of the reflected light, as a proportion of the incident light, is given by

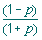where p is the ratio of the refractive indices of the two materials (n₁/n₂). Intensity is the square of this expression. The amount of reflected light is therefore larger when the disparity between the two refractive indices is greater. For an air/glass interface with the glass having a refractive index of 1.5, the intensity of the reflected light will be 4% of the incident light. For an optical system containing ten such surfaces, this shows that the transmitted beam will be attenuated to 66% of the incident beam from reflection losses alone.
Incidence Angle
The intensity of reflected and transmitted beams is also a function of the angle of incidence. Because of refraction effects, it is necessary to consider internal and external reflection separately at this point. External reflection is defined as reflection at an interface where the incident beam originates in the material of lower refractive index (i.e., air in the case of an air/glass or air/water interface). Internal reflection refers to the opposite case.
External Reflection at a Dielectric Boundary
Fresnel's laws of reflection precisely describe amplitude and phase relationships between reflected and incident light at a boundary between two dielectric media. It is convenient to think of incident radiation as the superposition of two plane-polarized beams, one with its electric field parallel to the plane of incidence (p-polarized) and the other with its electric field perpendicular to the plane of incidence (s-polarized). Fresnel's laws can be summarized in the following two equations which give the reflectance of the s- and p-polarized components:


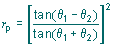In the limit of normal incidence in air, Fresnel's laws reduce to the following simple equation:

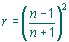It can easily be seen that, for a refractive index of 1.52 (crown glass), this gives a reflectance of 4%. This important result shows that about 4% of all illumination incident normal to an air-glass surface will be reflected. In a multielement lens systems, reflection losses would be very high if antireflection coatings were not used. The variation of reflectance with angle of incidence for both the s- and p-polarized components, plotted using the formulae above, is shown in the figure below.

External reflection at a glass surface (n=1.52) showing s- and p-polarization components
It can be seen that the reflectance remains close to 4% over about 30 degrees incidence, and that it rises rapidly to 100% at grazing incidence. In addition, note that the p-component vanishes at 56° 39'. This angle, called Brewster's angle, is the angle at which the reflected light is completely polarized. 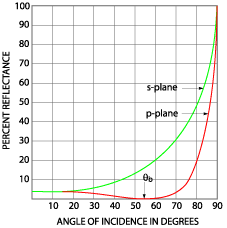This situation occurs when the reflected and refracted rays are perpendicular to each other (q₁+ q ₂= 90º ), as shown in the figure below.

At Brewster's angle the p-polarized component is completely absent in the reflected ray
This leads to the expression for Brewster's angle, q_B:

Under these conditions, electric dipole oscillations of the p-component will be along the direction of propagation and therefore cannot contribute to the reflected ray. At Brewster's angle, reflectance of the s-component is about 15%.
Internal Reflection at a Dielectric Boundary
For light incident from a higher to a lower refractive index medium, we can apply the results of Fresnel's laws in exactly the same way. The angle in the high-index material at which polarization occurs is smaller by the ratio of the refractive indices in accordance with Snell's law. The internal polarizing angle is 33° 21' for a refractive index of 1.52, corresponding to the Brewster angle (56° 39') in the external medium, as shown in the figure below.

Internal reflection at a glass surface (n=1.52) showing s- and p-polarized components
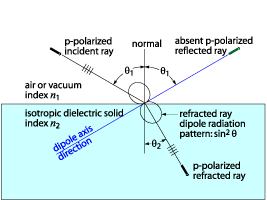
The angle at which the emerging refracted ray is at grazing incidence is called the critical angle (see the figure below). For an external medium of air or vacuum (n = 1), the critical angle is given by

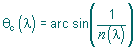and depends on the refractive index n (l), which is a function of wavelength. For all angles of incidence higher than the critical angle, total internal reflection occurs.
Phase Changes on Reflection
There is another, more subtle difference between internal and external reflections. During external reflection, light waves undergo a 180-degree phase shift. No such phase shift occurs for internal reflection (except in total internal reflection). This is one of the important principles on which multilayer films operate.
Interference
Quantum theory shows us that light has wave/particle duality. In most classical optics experiments, it is generally the wave properties that are most important. With the exception of certain laser systems and electro-optic devices, the transmission properties of light through an optical system can be well predicted and rationalized by wave theory. One consequence of the wave properties of light is that waves exhibit interference effects. Light waves that are in phase with each other undergo constructive interference, as shown below.

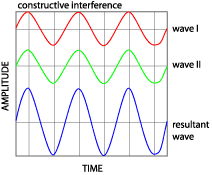
A simple representation of constructive interference
Light waves that are exactly out of phase with each other (by 180 degrees or p radians) undergo destructive interference, as shown below, and their amplitudes cancel. In intermediate cases, total amplitude is given by the vector resultant, and intensity is given by the square of amplitude.

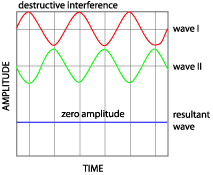
A simple illustration of destructive interference
Various experiments and instruments demonstrate light interference phenomena. Some interference effects are possible only with coherent sources (i.e., lasers), but many are produced by incoherent light. Three of the best-known demonstrations of visible light interference are Young's slits experiment, Newton's rings, and the Fabry-Perot interferometer. These are described in most elementary optics and physics texts. In all of these demonstrations, light from a source is split in some way to produce two similar wavefronts. The wavefronts are recombined with a variable path difference between them. Whenever the path difference is an integral number of half wavelengths (and if the wavefronts are of equal intensity), they cancel by destructive interference (i.e., an intensity minimum is produced). An intensity minimum is still produced if the interfering wavefronts are of differing amplitude; the result is just non-zero. When the path difference is an integral number of wavelengths, their intensities sum by constructive interference, and an intensity maximum is produced.
Thin-Film Interference
Thin-film coatings also rely on the principles of interference. Thin films are dielectric or metallic materials whose thickness is comparable to, or less than, the wavelength of light. When a beam of light is incident on a thin film, some of the light will be reflected at the front surface, and some of light will be reflected at the rear surface, as shown in the figure below. The remainder will be transmitted. At this stage, we shall ignore multiple reflections.

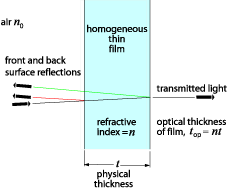
Front= and back-surface reflections for a thin film at near-normal incidence
The two reflected wavefronts can interfere with each other. This will depend on the ratio of optical thickness of the material and the wavelength of the incident light (click here for illustration). The optical thickness of an element is defined as the equivalent vacuum thickness (i.e., the distance that light would travel in vacuum in the same amount of time as it takes to traverse the optical element of interest). In other words, the optical thickness of a piece of material is the thickness of that material corrected for the apparent change of wavelength passing through it.

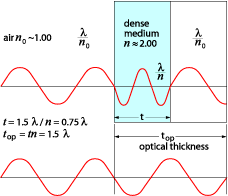
An illustration of the effects of lower light velocity in a dense medium. In this example, the velocity of light is halved in the dense medium, n=n/ n₀, and the optical thickness of the medium is 2x the real thickness
The optical thickness is given by t_o_p = t x n, where t is the physical thickness, and n is the ratio of the speed of light in the material to the speed of light in vacuum:

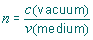To a very good approximation, n is the refractive index of the material. Returning to the thin film at normal incidence, the phase difference between the reflected wavefronts is given by (t_o_p/l) x 2p, where l is the wavelength of light, as usual, plus any phase differences caused by reflections at the surfaces. Clearly, if the wavelength of the incident light and the thickness of the film are such that a phase difference exists between reflections of p, then reflected wavefronts interfere destructively, and overall reflected intensity is a minimum. If the two reflections are of equal amplitude, then this amplitude (and hence intensity) minimum will be zero. In the absence of absorption or scatter, the principle of conservation of energy indicates all "lost" reflected intensity will appear as enhanced intensity in the transmitted beam. The sum of the reflected and transmitted beam intensities is always equal to the incident intensity. This important fact has been confirmed experimentally. Conversely, when the total phase shift between two reflected wavefronts is equal to zero (or multiples of 2p), then the reflected intensity will be a maximum, and the transmitted beam will be reduced accordingly.

Previous Next